КОНТАКТ ТВЁРДЫХ ТЕЛ

Поскольку реальный профиль поверхностей отличается от номинального, заданного чертежом, контакт твердых тел также отличается от номинального и осуществляется за счет сближения этих тел путем деформации отдельных микронеровностей на контактиру­ющих поверхностях — волн и микровыступов. Поэтому реальный контакт трущихся тел всегда дискретен, так что механический контакт твердых тел представляет собой совокупность пятен контакта, через которые эти тела прижимаются друг к другу.

К тому же приходится учитывать три разновидности площади контакта: номинальная А_a (НПК), фактическая A_r (ФПК) и контурная A_c (КПК).

Номинальная площадь контакта A_a ограничена геометрическими очертаниями площади контакта и представляет собой геометрическую площадь соприкосновения контактирующих тел (рис.1), т.е. для прямоугольного очертания такой площадки длиной а и шириной b будем иметь А_a = ab.

Контурная площадь контакта А_с формируется в результате деформации (обычно, упругой) элементов волнистости поверхностей кон­тактирующих тел в процессе смятия вершин этих элементов

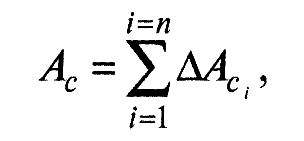(1)

где ΔА_сi – площадка, образованная деформацией отдельного элемента волнистости.

Фактическая площадь контакта A_r формируется в результате де­формирования вершин микровыступов сопряженных поверхностей. Эти деформированные микровыступы (см. рис. 1) расположены на контурных площадках контакта, ограниченных ее площадью.

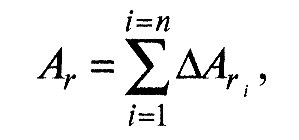(2)

где  ΔAri – площадка, образованная деформацией отдельного микровыступа.

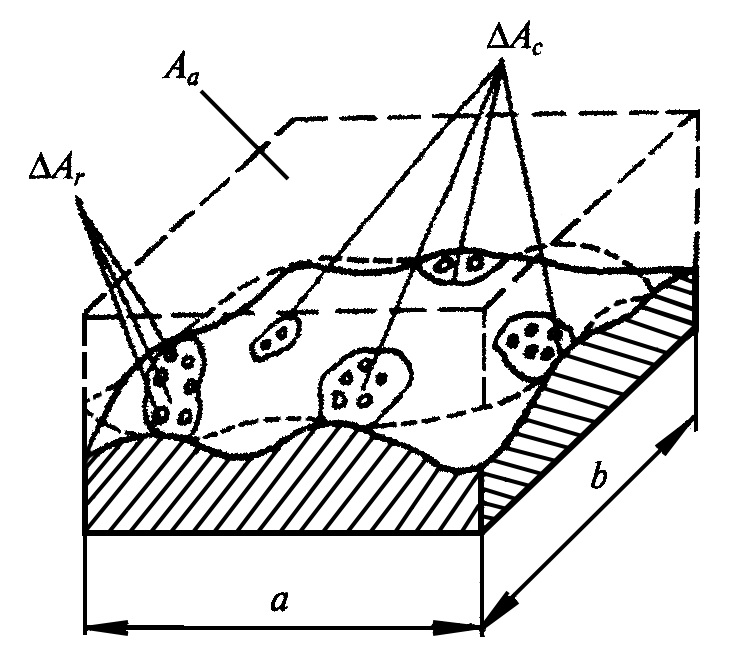
Рис.1. Схема контакта шероховатых поверхностей: А_а – номинальная площадь контакта; ΔA_c – единичная площадка контурного  контакта; ΔA_r – единичная площадка фактического контакта.

Следует учитывать, что фактическая площадь контакта составляет незначительную долю от номинальной площади контакта (от сотых и даже тысячных долей до 20-40%)

Соответственно трем видам площадей контакта различают три вида контактных давлений: номинальное ра, контурное р_с и фактическое р_r:

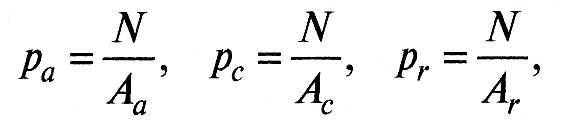(3)

где N – сила, действующая на контактирующие тела.

Определение этих давлений необходимо для большинства расчетов в трибологии.

Поскольку реальный контакт осуществляется по ФПК, то его определению придается особое значение. Как уже показано, контакт шероховатых тел имеет дискретный характер. Опыт показывает, что отдельные микровыступы по форме близки к полусферическим сегментам и ФПК представляет собой сумму элементарных пятен контакта, образовавшихся в результате деформирования (упругого или пластического) этих сегментов. Поэтому модель шероховатого слоя представлена И.В. Крагельским и Н.Б. Демкиным в виде набора сегментов полусферической формы, имеющих одинаковый радиус, но расположенных по высоте на различном уровне так, чтобы распределение материала по высоте соответствовало распределению материала в реальном шероховатом слое, а площадь сечения выступов в горизонтальной плоскости при различных уровнях сближения (рис. 2) соответствовала экспериментально определяемой кривой опорной поверхности t_p.

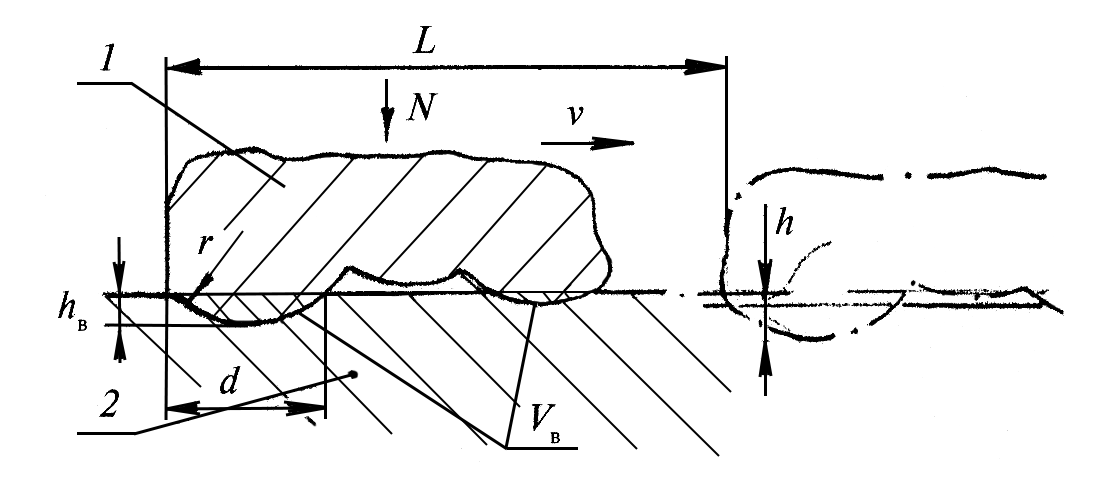
Рис. 2. Модель контакта жесткого шероховатого недеформируемого тела 1 с деформируемым идеально гладким телом 2: h_B – глубина внедрения; d и r – диаметр полусферической неровности и радиус закругления ее вершины; h – деформация тела 2; V_B – объем материала тела 2, выдавленный единичной неровностью тела 1; L – длина пути тела 1 по телу 2; N – сила, действующая на контактирующие тела.

Средний радиус кривизны вершин выступов r представляет собой среднее значение кривизны вершин выступов, определенное для пяти наиболее высоких выступов в пределах базовой длины. Радиусы кривизны выступов определяют из профилограммы, снятых в направлении, перпендикулярном следам механической обработки, и в направлении следов обработки. Средний радиус кривизны отдельной неровности r_i определяется по длине сечения выступа d на расстоянии h от вершины неровности по приближенной формуле

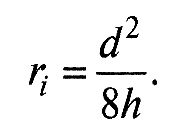 (4)

В трибологических расчетах используют значение приведенного радиуса кривизны вершин выступов

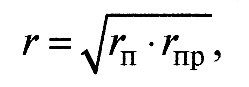 (5)

где r_п и r_пр – радиусы кривизны вершин выступов в поперечном и продольном направлениях, соответственно.

Значения r в зависимости от режима механической обработки меняются от 15-55 мкм при точении и от 5-18 мкм при внутреннем шлифовании, до 230-670 мкм при полировании и 300-3000 мкм при доводке плоских поверхностей.

По характеру деформации контакт может быть упругим, упруго-пластическим и пластическим. При упругом контакте при снятии нагрузки форма деформированных неровностей восстанавливается полностью; при упруго-пластическом контакте – лишь частично, и при пластическом контакте не восстанавливается совсем:

а) при упругом контакте р_r < с_дσ_т, где σ_т – предел текучести более мягкого материала трибосопряжения, с_д – коэффициент, учитывающий форму деформируемых неровностей. Экспериментально-теоретические исследования показали, что для сферы с_д ~ 3, но Зσ_т ~ НВ, где НВ — твердость по Бринеллю. Следовательно, при р_r < НВ контакт упругий;

б) при пластическом контакте р_r > с_дσ_т или р_r > НВ. Установлено, что при пластическом контакте обычно пластичны только микрошероховатости, тогда как волны деформируются упруго;

в) при упруго-пластическом контакте соотношение между напряженностью контакта и твердостью по Бринеллю занимает промежуточное положение.

По уровню насыщенности контакт может быть:

а) ненасыщенный – формируется, когда деформируемые неровности не оказывают друг на друга влияния, поскольку расположены далеко друг от друга. По мере роста нагрузки площадь контакта увеличивается, главным образом, путем увеличения числа вступающих в контакт вершин микронеровностей. В этом случае расчеты площадей контакта производят с учетом только начального участка кривой опорной поверхности;

б) насыщенным – имеет место, когда деформируемые неровности расположены столь близко друг от друга, что на их деформирование влияет присутствие соседних неровностей, и увеличение площади контакта происходит за счет роста элементарных участков контакта, т.е. величины d. Тогда кривую опорной поверхности рассчитывают по формуле:

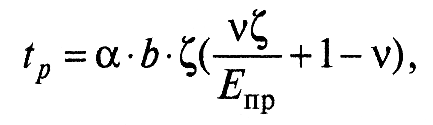(6)

где α – коэффициент усадки; Е_пр – приведенный модуль упругости.

Контакт считается полностью насыщенным, когда А_r становится равным А_с.

Расчет давлений на фактическом пятне контакта. Критерий Гринвуда-Уильямсона. Прежде чем рассчитывать фактическое давление, необходимо оценить вид контакта, т.е. выяснить, следует его рассчитывать по формуле для упругого или пластического контакта. Предварительная оценка характера деформации производится по критерию Гринвуда-Уильямсона (индексу пластичности):

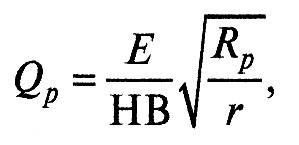 (7)

где Е – модуль упругости; НВ – твердость по Бринеллю; R_p – высота сглаживания; r – радиус единичной неровности.

Если Q_p > 3, то контакт пластический; если меньше – то упругий. Руководствуясь этим, следует выбрать уравнение для расчета величины давления на фактической площади контакта.

Примечание. Здесь и во всех последующих расчетах следует:

а) учитывать параметры шероховатости и волнистости более твердого тела, а твердость – более мягкого. При упругом контакте принимать значение модуля упругости для того тела, для которого он меньше;

б) если шероховатость сопряженных тел одного порядка, то следует брать для расчета эквивалентные значения параметров: v_1,2; R_p1,2; t_m1,2 и т.д., учитывая микрогеометрию и первой, и второй поверхностей. Так,

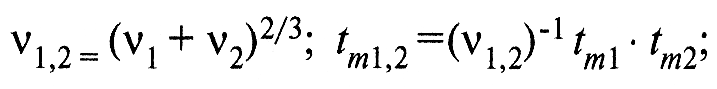
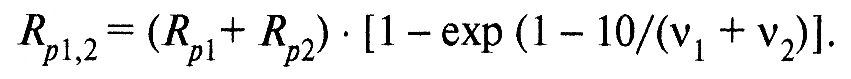(8)

Расчет давлений на фактической площади контакта при упругой деформации. При упругом контакте единичной сферы с деформируемым полупространством величины деформаций, контактных давлений и площадей контакта рассчитываются по формуле Герца.

При упругом множественном контакте давления на ФПК рассчитывают по формуле:

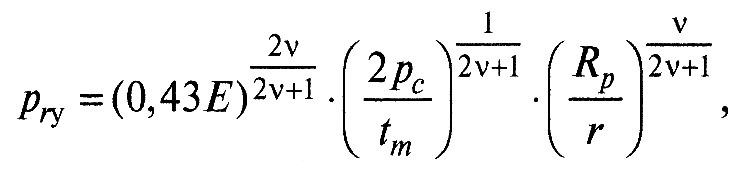(9)

где Е – модуль упругости; r – приведенный радиус кривизны вершин неровностей; р_с – контурное давление, определяемое по формуле.

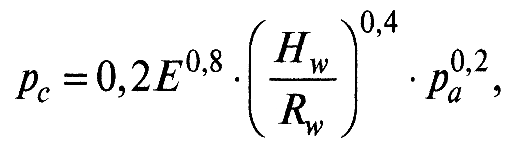(10)

где H_w и R_w – соответственно высота и радиус волны, рa – номинальное давление.

При наиболее распространенных в машиностроении видах механической обработки поверхностей трения t_m = 0,5, v = 2. Тогда

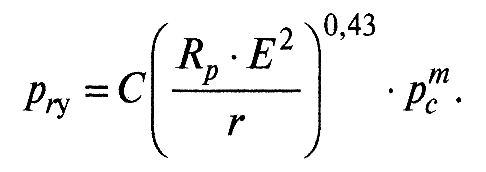(11)

При контактировании двух шероховатых поверхностей С = 0,61; m = 0,14. При контактировании гладкой и шероховатой поверхности С = 0,86; m = 0,2.

Расчет давлений на фактической площади контакта при пластической деформации. При расчете контактных давлений в условиях пластического контакта рекомендуется формула:

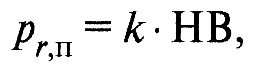(12)

где для неупрочняемых материалов k = 1; для упрочняемых k =1,3.

Если силой N осуществляется повторное нагружение контакта, ранее пластически деформированного силой N₀, то при N ≤ N₀ деформация будет упругой и давление на ФПК рассчитывается по формуле:

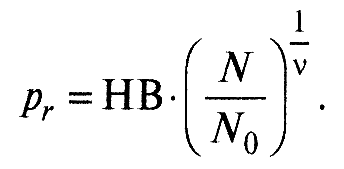(13)

Расчет величины сближения. Взаимное сближение δ контактирующих тел при их совместном деформировании определяется следующим образом:

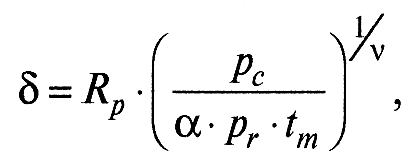(14)

где α – коэффициент усадки выступов. Для абсолютно упругого тела α = 0,5; для абсолютно пластичного α = 1.

Другие характеристики контакта, которые рассчитываются из значения р_r:

• фактическая площадь контакта

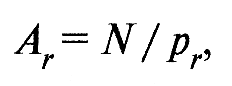(15)

где N – нормальная нагрузка на узел трения.

• число пятен фактического контакта

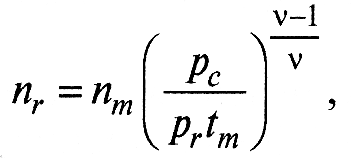(16)

где n_m – число выступов, вершины которых лежат выше средней линии.

В заключение необходимо отметить следующее:

1. В значение усилия N, прижимающего друг к другу контактирующие тела, определенный вклад вносит адгезия этих тел. Это становится заметным при сближении их контактирующих поверхностей на расстояния действия межмолекулярных сил и при относительно низких нагрузках. Это следует учитывать при расчетах.
2. Фактическая площадь контакта взаимодействующих тел и при неподвижном состоянии, и при относительном перемещении одного тела по другому практически одинакова. В то же время величина внедрения единичной неровности при ее перемещении по деформируемому полупространству приблизительно вдвое превышает внедрение в статическом состоянии, что и следует из геометрии трибоконтакта.
3. В ряде случаев необходимо учитывать динамические характеристики контакта трущихся тел. Узлы трения не только подвергаются динамическим воздействиям извне, но и сами могут явиться источником этих воздействий.

Литература

1.  Доценко А.И., Буяновский И.А. / Основы триботехники. Учебник. - М.: Инфра-М, 2014.
2.  Крагельский И.В., Михин Н.М. Узлы трения машин : справочник  - Москва: Машиностроение, 1984.
3.  Трение, изнашивание и смазка: Справочник. В 2-х кн. / Под ред. И.В. Крагельского, В.В. Алисина. - М.: Машиностроение, 1978, Кн.1
4.  А.В. Чичинадзе, Э.Д. Браун, Н.А. Буше и др.; Под общ. ред. А.В. Чичинадзе. / Основы трибологии (трение, износ, смазка).  2-е изд. переработ, и доп. - М.: Машиностроение, 2001.