ТРЕНИЕ СКОЛЬЖЕНИЯ

Трение скольжения является наиболее распространенным видом трения. Основной характеристикой трения скольжения является сила трения.

Сила трения - это сила сопротивления относительному перемещению одного тела по поверхности другого под действием внешней силы, тангенциально направленная к общей границе между двумя телами.

Поскольку поверхность контакта дискретна, взаимодействие трущихся тел осуществляется на изолированных друг от друга участках фактической площади контакта, а сила трения - равнодействующая всех элементарных сил сопротивления перемещению на этих пятнах.

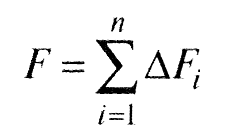(1)

где ΔF_i - элементарная сила трения на i-м дискретном контакте.

Схема контакта трущихся тел при трении скольжения приведена на рис.1. Сила трения направлена противоположно направлению относительного движения контактирующих тел.

При переходе от состояния покоя к состоянию движения имеет место состояние предварительного смещения.

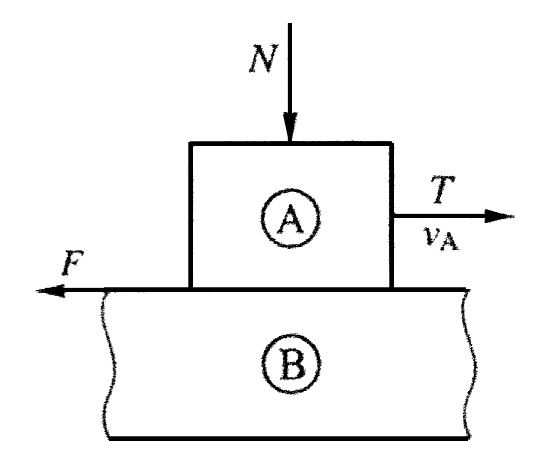
Рис.1. Схема контакта трущихся тел A и B: N - нормальная нагрузка; T - тангенциальное усилие; F - сила трения.

Предварительное смещение

В соответствии с существованием трения покоя и трения движения различают силу трения покоя и силу трения движения, количественно оценивающие эти процессы. Изменение силы трения при переходе от покоя к движению контактирующих тел по мере перемещения одного тела относительно другого иллюстрирует рис.2. При трогании неподвижного тела с места движению предшествует стадия предварительного смещения.

 

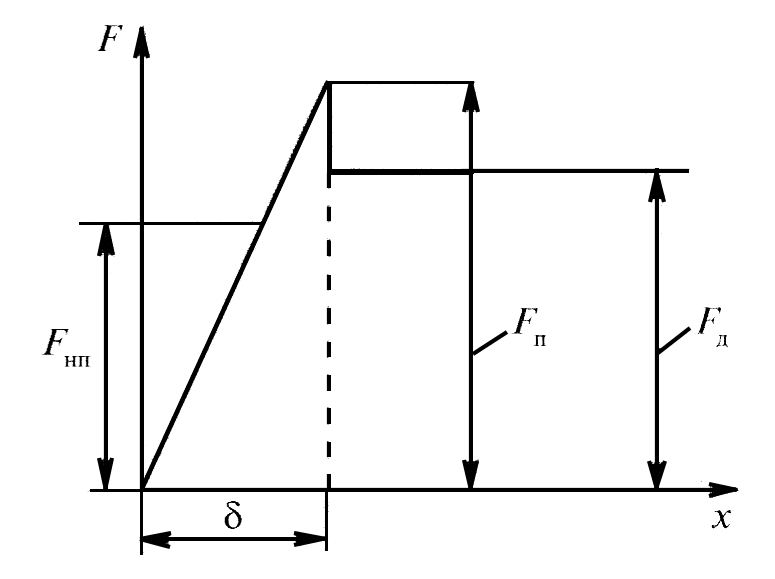
Рис.2. Изменение силы трения в зависимости от величины перемещения x.

Предварительное смещение - относительное микросмещение двух твердых тел в пределах от состояния покоя до начала относительного движения.

Развиваемая по мере увеличения микросмещения неполная сила трения покоя F_нп возрастает до тех пор, пока не будет достигнута полная сила трения F_п, превышение которой ведет к началу макросмещения, т.е. трение покоя скачкообразно сменяется трением движения F_д и начинается непрерывное перемещение одного тела относительно другого. Имеет первоначально упругий характер, т.е. прекращение действия сдвигающей силы T (см. рис.1) ведет к возврату в положение равновесия.

Развиваемая при микросмещении полная сила трения покоя для несмазываемых тел F_п почти всегда выше силы трения движения F_д.

Законы Амонтона для трения скольжения

При рассмотрении процесса трения скольжения в качестве первого приближения используют экспериментально установленные еще Амонтоном (1699) закономерности, известные в литературе как законы Амонтона.

1. Сила трения F пропорциональна усилию N, сжимающему трущиеся тела в направлении, нормальном к поверхности трения (Поверхностью трения называют номинальную поверхность твердого тела, по которой осуществляется взаимодействие твердых тел при внешнем трении)

F = f·N. (2)

Коэффициент пропорциональности f в этом уравнении называют коэффициентом трения. Иначе говоря, коэффициент трения - отношение силы трения двух тел к нормальной силе, прижимающей эти тела друг к другу. Коэффициент трения является важнейшей сравнительной характеристикой, позволяющей сопоставлять трение различных тел в разных условиях безотносительно к нагрузке на узел трения.

2. Сила трения не зависит от номинальной площади контакта трущихся твердых тел.

В процессе развития триботехники было установлено, что область применения законов Амонтона ограничена. Так, независимость коэффициента трения от нагрузки, следующая из приведенного уравнения, нарушается в области очень малых и достаточно больших нагрузок. Закон Амонтона нарушается также для очень твердых тел (алмаз) и очень упругих тел (резина). Коэффициент трения этих материалов уменьшается с увеличением нагрузки. Номинальная площадь контакта трущихся тел может влиять на величину силы трения для материалов, обладающих вязкоупругими свойствами, а также в тех случаях, когда она оказывает влияние на поступление среды в трибоконтакт.

Механизм внешнего трения

В общем случае коэффициент трения зависит от большого числа факторов (напряженно-деформированного состояния фрикционного контакта, механических и физико-химических свойств поверхностного слоя контактирующих тел, окружающей среды, в том числе смазочного материала, конструктивных особенностей сопряжения, режима работы узла трения и т.д.) и определяется в основном взаимодействием поверхностных слоев твердых тел, вовлеченных в трибологический контакт, между собой и взаимодействием рабочих поверхностей твердых тел со средой, включая смазочный материал.

Взаимодействие твердых тел в процессе трения развивается в микрообъемах, образующихся в зоне касания этих тел. По И.В. Крагельскому, в местах касания возникают фрикционные связи (т.е. пятна контакта, которые образуются и существуют лишь при совместном действии нормальных и тангенциальных сил в фрикционном контакте), образующие некоторое «третье тело». Это третье тело включает в себя измененный материал обоих контактирующих тел, наделенный своим химическим составом, напряженным состоянием и структурой. И.В. Крагельский при анализе трибологического процесса выделяет три этапа:

• образование фрикционной связи;
• существование фрикционной связи, обусловленное изменениями, протекающими на поверхностях трения (направление этих изменений определяется принципом Ле Шателье-Брауна) в результате указанных взаимодействий;
• нарушение фрикционных связей, приводящее к разрушению поверхностей.

В том случае, если разрыв фрикционных связей происходит внутри «третьего тела», имеет место внешнее трение. При этом должно соблюдаться такое соотношение прочностных свойств «третьего тела» и свойств материала трущихся тел в объеме, при котором прочность на сдвиг возрастает по мере удаления от поверхности вглубь основного материала (сформулированное И.В. Крагельским правило положительного градиента механических свойств по глубине, характеризуемое отношением dτ_кр/dτ>0). При этом важно не только соотношение сдвиговых прочностей в тончайшем поверхностном слое («третье тело») и в объеме тел, но и геометрические характеристики трибологического контакта (безразмерная глубина зоны деформации). Это соотношение называется порогом внешнего трения. Для сферической модели неровностей это соотношение имеет вид:

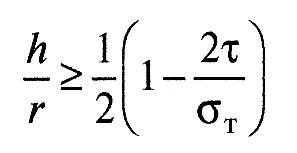 (3)

где h - глубина внедрения единичной неровности в деформируемое тело, r - радиус этой неровности, τ - сдвиговая прочность фрикционной связи; σ_τ - предел текучести деформируемого материала.

При нарушении этого соотношения имеет место переход от внешнего трения к внутреннему, характеризуемому интенсификацией разрушения поверхностных слоев контактирующих тел.

Распределение областей локализации внешнего и внутреннего трения иллюстрирует рис.3.

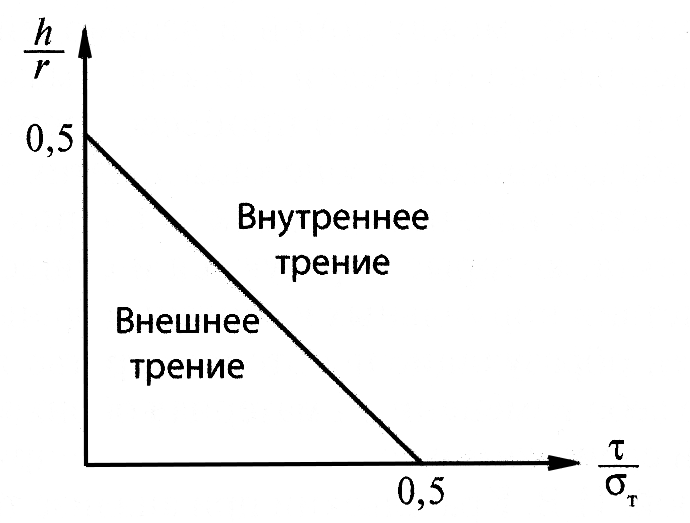
Рис.3. Области локализации внешнего и внутреннего трения (по Польцеру и Майснеру)

На процесс внешнего трения влияет большое количество факторов. но в конечном счете основную роль играет взаимодействие твердых тел между собой на участках трибологического контакта. Это взаимодействие заключается в преодолении сил молекулярного притяжения (адгезии) между контактирующими телами на пятнах (элементарных участках) площади фактического контакта, а также в формоизменении рельефа контактирующих тел в результате их упругих и пластических деформаций их поверхностных слоев. Таким образом, трение определяется процессами деформации поверхностных слоев и адгезией контактирующих тел в результате их межмолекулярного взаимодействия.

Согласно молекулярно-механической теории И.В. Крагельского, силу трения можно рассматривать как сумму адгезионной и деформационной составляющих

F = F_адг + F_деф, (4)

где F_адг и F_деф - адгезионная и деформационная составляющие силы трения, действующие на элементарных пятнах контакта.

Расчет коэффициента трения

Наиболее распространенной характеристикой процесса трения является величина коэффициента трения f, равная отношению силы трения F двух тел к нормальной силе N, прижимающей эти тела друг к другу. В таком случае

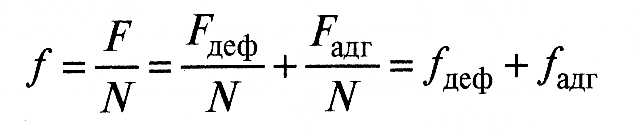(5)

т.е. коэффициент трения имеет две составляющие - деформационную и адгезионную. Рассмотрим расчет коэффициента трения двух тел применительно к контакту единичной неровности с деформируемым полупространством и коэффициента трения при множественном контакте.

Расчет коэффициента трения при контакте единичной неровности, сводится к определению его деформационной и адгезионной составляющих.

Деформационная составляющая для единичного контакта определяется глубиной относительного внедрения h/r, т.е. отношения глубины h внедрения сферической неровности к радиусу r этой неровности (рис.4). Значение деформационной составляющей рассчитывают для пластического контакта единичной неровности с деформируемым телом по формуле:

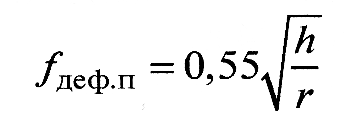 (6)

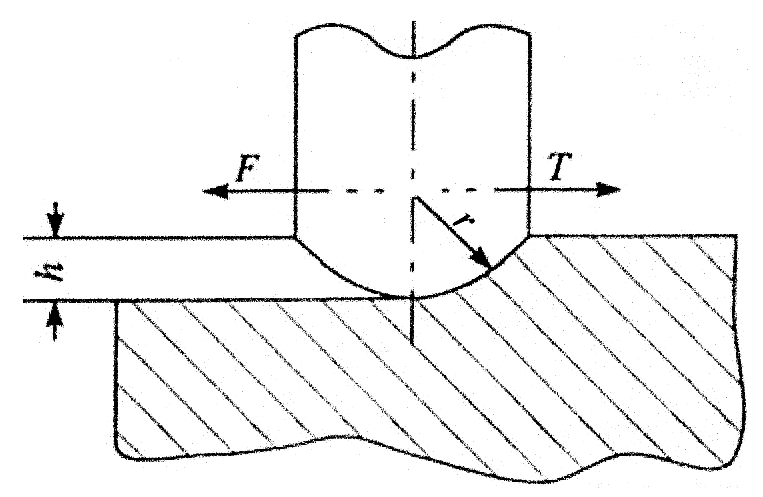
Рис.4. Схема и вычисление деформационной составляющей коэффициента трения.

и для упругого контакта этого сопряжения по формуле:

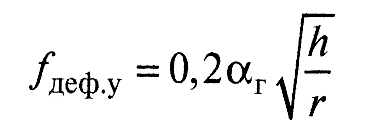 (7)

где α_т - коэффициент гистерезисных потерь (α = 22α*, где α* - гистерезисные потери при одноосном растяжении, причем для металлов α_г* = 0,01...0,14; для пластмасс и резин α_г* = 0,09...0,35).

Адгезионная составляющая коэффициента трения подчиняется биноминальному закону:

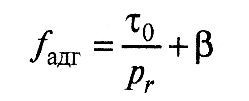 (8)

где τ₀ - удельная сдвиговая прочность молекулярных связей при нулевом фактическом давлении; β - коэффициент упрочнения адгезионных связей под воздействием нормальных сжимающих напряжений; p_r - фактическое давление в контакте.

Биноминальный закон трения следует из представления о существовании «третьего тела», которое в процессе трения находится в состоянии непрерывного формоизменения, «течет» подобно жидкости в узком зазоре между двумя телами, перемещающимися одно относительно другого. При этом исходят из допущения пропорциональности сопротивления сдвигу единичной частицы «третьего тела» и времени ее оседлой жизни по уравнению Френкеля-Журкова (рис.5).

Следует иметь в виду, что в несколько иной форме и из совершенно иных представлений биноминальный закон трения был выведен Б.В. Дерягиным еще в 1934 г.

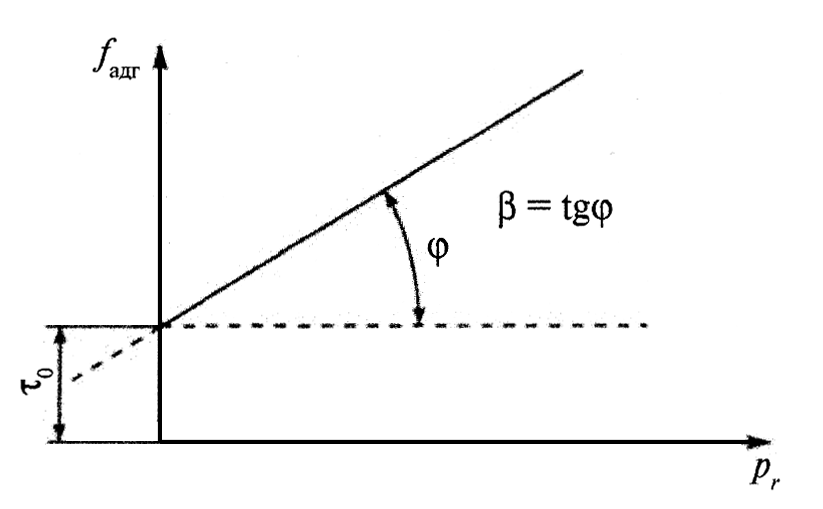
Рис.5. Зависимость адгезионной составляющей коэффициента трения (удельного сдвигового сопротивления) и f_адг от фактического давления p_r.

Определение величин τ₀ и β производится экспериментально.

Значения τ₀ и β для ряда распространенных материалов табулированы (табл.1). Это позволяет рассчитывать коэффициенты трения этих материалов для различных условий контакта и разной микрогеометрии поверхностей контактирующих тел.

Таблица 1. Параметры сдвиговой прочности молекулярных связей при трении по закаленной стали (по И.В. Крагельскому и Н.М. Михину)

№ п/п	Материал	τ0, МПа	β
1	Свинец	3,6	0,057
2	Серебро	10,0	0,081
3	Медь	15,0	0,08
4	Олово	5,0	0,068
5	Индий	1,5	0,066

Для приработанных поверхностей коэффициент трения не зависит от нагрузки и может быть рассчитан из уравнения:

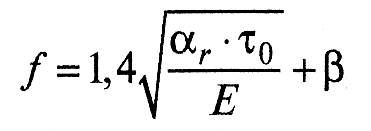 (9)

где E - модуль упругости деформируемого тела.

Интересно отметить, что, согласно Ю.Н. Васильеву, коэффициент β характеризует долю работы сил трения, затраченной на изнашивание трущихся тел.

Таким образом, суммарный коэффициент трения на единичном пятне контакта

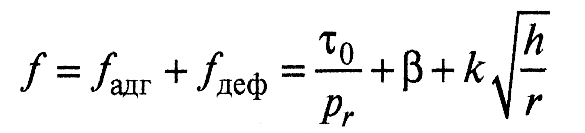 (10)

где для пластического контакта k=0,55; для упругого k=0,2α_г.

Расчет коэффициента трения для множественного контакта. Для ансамбля неровностей силы трения на единичных пятнах контакта суммируются и для множественного контакта силы трения рассчитывают по формуле:

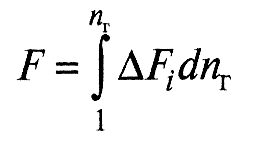 (11)

где ΔF_i - сила трения, возникающая на единичной произвольной микронеровности; n_г - число микронеровностей, внедрившихся на одинаковую глубину.

После ряда подстановок и несложных преобразований отсюда получены уравнения для расчета коэффициента трения при различных видах фрикционного контакта. Такое уравнение имеет вид:

• для ненасыщенного упругого контакта

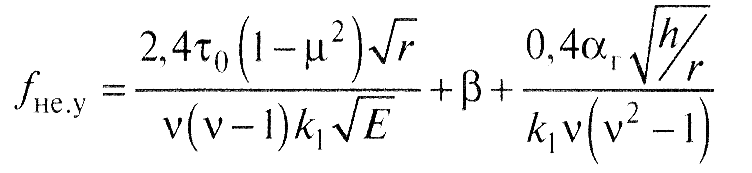 (12)

• для насыщенного упругого контакта

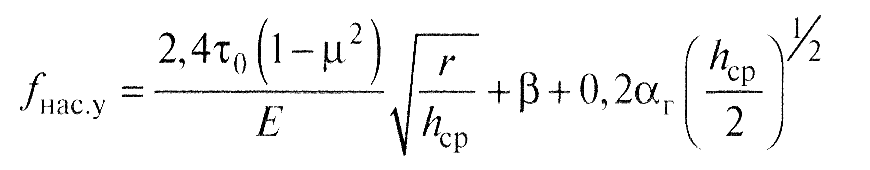 (13)

• для ненасыщенного пластического контакта

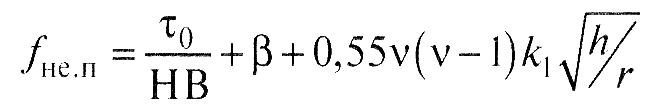 (14)

• для насыщенного пластического контакта

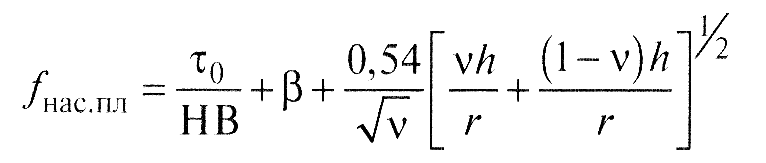 (15)

В приведенных выше расчетных уравнениях: τ₀ и β - фрикционные константы, зависящие от физико-химического состояния поверхностей контактирующих тел; α_г - коэффициент гистерезисных потерь; ν - параметр опорной кривой профиля поверхности; k₁ - коэффициент, зависящий от параметра ν (рис.6); E - модуль упругости деформируемого тела; µ - коэффициент Пуассона; h - величина сближения поверхностей (глубина внедрения единичной неровности); r - радиус неровности, моделируемой сферой; h_ср - средняя величина внедрения.

Анализ приведенных уравнений показывает, что в них учтены физико-механические свойства контактирующих тел: в уравнениях (12) и (13) - через величины E, µ,  α_г; в уравнениях (14) и (15) - через величины HB; физико-химические свойства взаимодействующих поверхностей через значения параметров τ₀ и β, микротопография поверхностей через значения ν и r, параметры нагружения - через величины h - во всех уравнениях.

 

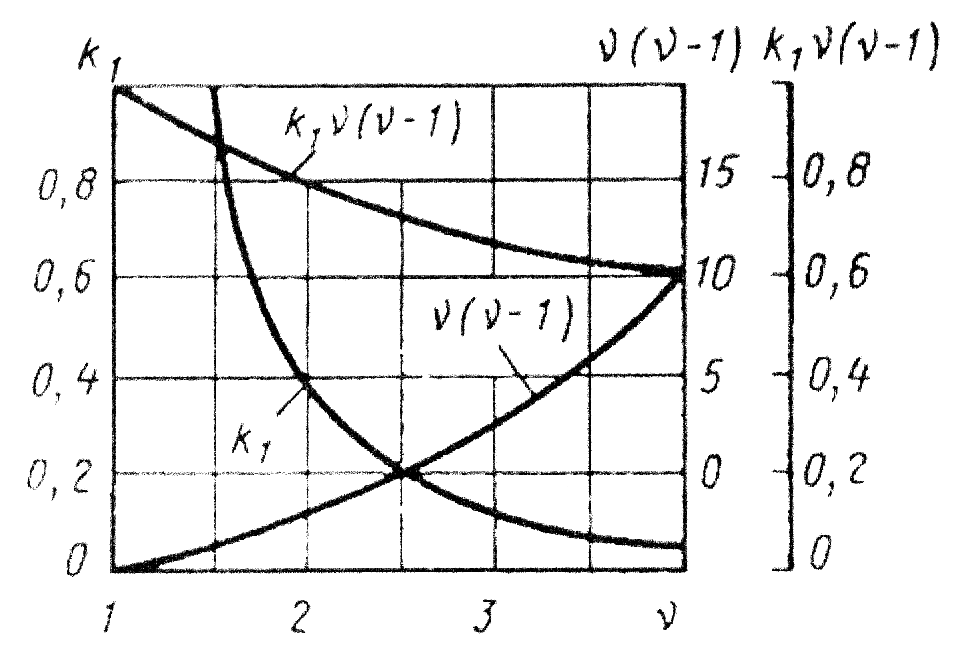
Рис.6. График для определения значений k_1'ν(ν-1) и k₁ν(ν-1) в зависимости от параметра ν.

Для приработанных поверхностей трение происходит в условиях упругого контакта; коэффициент трения при этом не зависит от нагрузки:

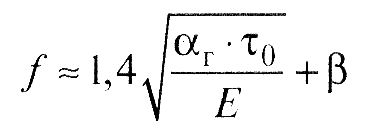 (16)

Факторы влияющие на трение скольжения.

1. Влияние на коэффициент трения таких факторов, как фрикционные константы τ₀ и β; физико-механические свойства поверхностей контактирующих тел - HB, E, µ, α_г; параметры, характеризующие микротопографию поверхностей - ν, r, t_m, R_p, k₁ параметр нагружения p_r можно оценить, исходя из уравнений (1)-(5).

2. Значительное влияние на коэффициент трения оказывают строение и физико-механические свойства контактирующих тел. Так, у одноименных металлов с кристаллической кубической решеткой (Al-Al; Cu-Cu; Fe-Fe) коэффициент трения выше, чем у металлов с гексагональной упаковкой (Cd-Cd; Mn-Mn; Zn-Zn) (рис.7).

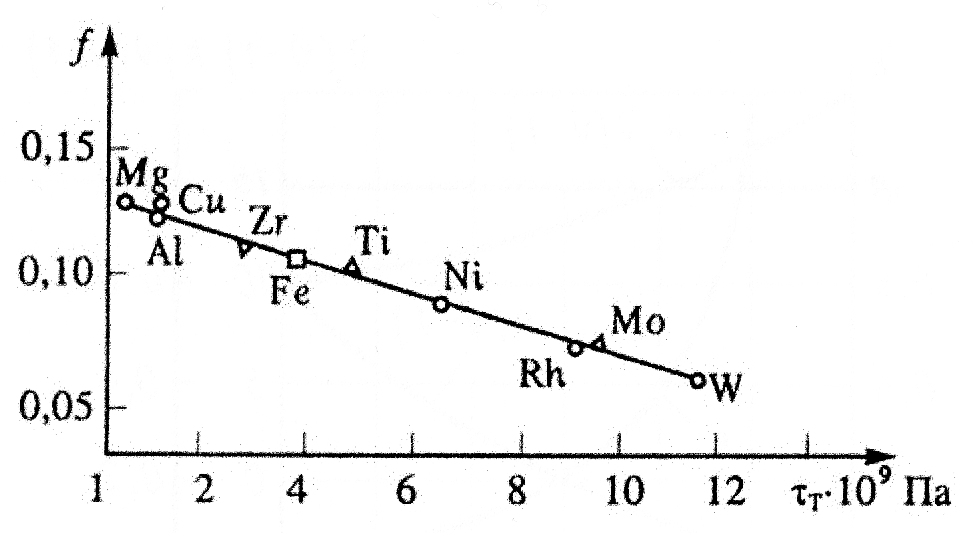
Рис.7. Зависимость коэффициента трения f от предела текучести на сдвиг τ_т для различных металлов.

3. Для пар трения из различных металлов коэффициент трения ниже, чем для одинаковых.

4. На коэффициент трения материалов значительное влияние оказывают природа образующихся на поверхности «вторичных структур» (например, оксидных пленок и т.д.) или заранее нанесенных тонких покрытий. Важно соотношение физико-механических свойств покрытия и подложки. Если металл мягок и эластичен, а оксид тверд и хрупок, то пленки легко разрушаются, и имеет место ювенальный контакт при малых нагрузках. Если металл имеет такие же деформационные свойства, как и его оксид, то эта пленка деформируется вместе с металлом не разрушаясь (например, Cu), обеспечивает снижение адгезионного эффекта и препятствует преодолению внешнего трения. Для обеспечения низкого коэффициента трения необходимо, чтобы поверхностная пленка обеспечивала полное разделение контактирующих поверхностей (обеспечение правила положительного градиента прочности по глубине), но не должна быть излишне толстой, чтобы избежать повышения деформационной составляющей коэффициента трения, так как в толстой пленке деформационная составляющая коэффициента трения становится заметной. На рис.8 это показано применительно к зависимости коэффициента трения закаленной стали по стали, покрытой пленкой индия, от толщины этого покрытия.

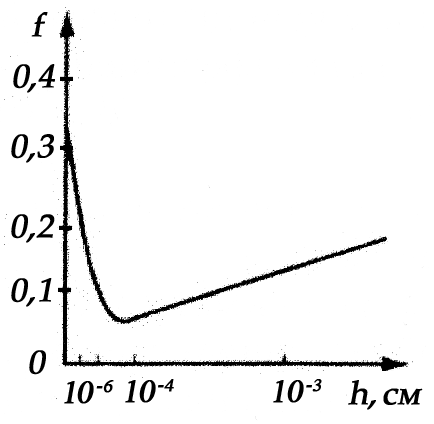
Рис.8. Зависимость коэффициента трения f стального сферического индентора радиусом 0,3 мм по инструментальной стали, покрытой пленкой индия, от толщины h этого покрытия.

Образование и разрушение вторичных структур оказывает большое влияние на коэффициент трения. Так, на зависимости коэффициента трения, согласно Б.И. Костецкому, можно выделить три участка (рис.9): участок I, на котором коэффициент трения достаточно высок, но по мере повышения нагрузки по ряду причин (в частности, вследствие активации поверхностей трения, облегчающей образование вторичных структур в трибологическом контакте) снижается до некоторой установившейся величины (переходный режим). На участке II зависимость f(N) трение подчиняется закону Амонтона, вследствие образования на поверхности трения вторичных структур, обеспечивающих наличие положительного градиента механических свойств по глубине. Участок II ограничен некоторой критической нагрузкой, при которой скорость разрушения вторичных структур превысит скорость их образования, так что правило И.В, Крагельского перестает выполняться, и имеет место переход к схватыванию, заеданию и другим патологическим процессам вплоть до сваривания контактирующих поверхностей, т.е. режим повреждаемости.

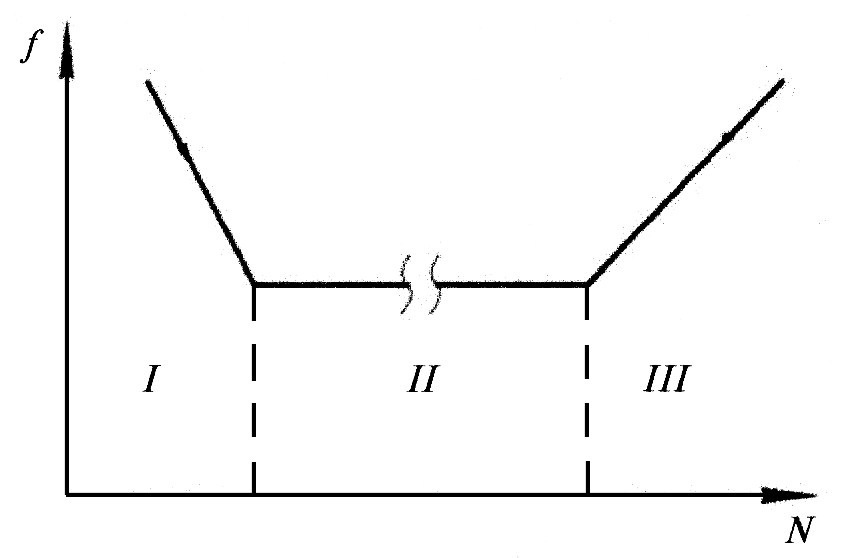
Рис.9. Схематическое изображение зависимости коэффициента трения от приложенной нагрузки: I - переходный режим; II - стационарный режим; III - режим повреждаемости.

Вследствие этого на участке III зависимости f(N) наблюдается резкий рост коэффициента трения, его скачкообразное изменение, поскольку при этом чередуется схватывание контактирующих поверхностей, разрушение образовавшихся при этом адгезионных соединений, проскальзывание и т.д.

Обобщенная зависимость коэффициента трения металлов от скорости относительного перемещения (в данном случае - скольжения) трущихся тел, согласно Б.И. Костецкому, также характеризуется тремя участками (рис.10): I - характеризующий нормальный режим стационарного трения; II - на котором реализуется патологический процесс, развивающийся при схватывании I рода (т.е. холодное заедание); III - на котором развиваются патологические процессы схватывания II рода (т.е. горячее заедание).

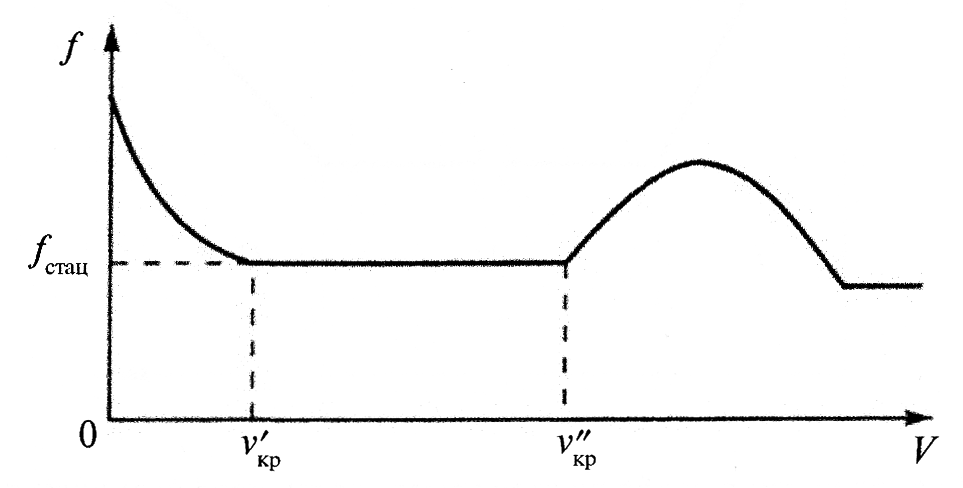
Рис.10. Схема изменения коэффициента трения f от скорости V относительного перемещения твердых тел.

Стационарный участок имеет место в диапазоне скоростей V'_кр и V''_кр, т.е. V'_кр ≤ 0 ≤ V''_кр, схватывание I рода имеет место при φ < V < V'_кр, схватывание II рода происходит при V > V''_кр.

Схватывание I рода возникает при трение скольжения с малыми скоростями относительного перемещения и удельными нагрузками, превышающими предел текучести на участках фактического контакта при отсутствии слоя смазочного материала или вторичных структур, разделяющих поверхности трения. Схватывание II рода также является процессом недопустимой повреждаемости поверхностей трения, выражающейся в образовании местных очагов схватывания, сваривания, причем этот процесс обусловлен размягчением, деформацией и контактированием ювенильных поверхностей трущихся тел. Этот процесс возникает при трении скольжения с большими скоростями и удельными нагрузками. Значительное тепловыделение может привести к существенному размягчению поверхностей и даже к их оплавлению, так что между трущимися телами может образоваться прослойка расплавленного металла, в результате чего трение даже снижается (участок справа от участка III на рис.10). На стационарном участке сила трения практически не изменяется во времени, на участках I и III сила трения скачкообразно изменяется во времени.

Зависимость f = φ(V) может при изменении условий процесса смещаться вверх или вниз, а стационарный участок может расширяться или сужаться, что определяется условиями образования вторичных структур, обеспечивающих существование стационарного участка.

Одним из наиболее сильно действующих на трение факторов является температура фрикционного сопряжения - как генерированная в процессе трения, так и полученная от внешнего источника тепла. При повышении температуры снижаются значения HB, τ₀, p_r, увеличивается глубина внедрения h. Как правило, при увеличении объемной температуры T_объемн адгезионная составляющая трения f_адг уменьшается, а деформационная f_деф - возрастает. В общем случае при росте объемной температуры коэффициент трения проходит через минимум (рис.11).

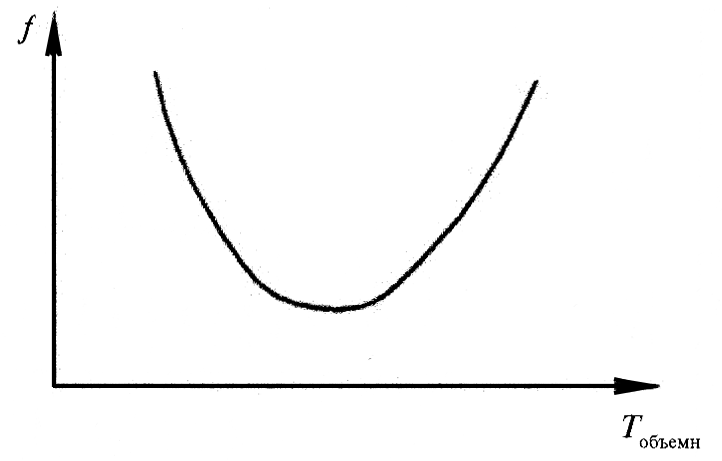
Рис.11. Влияние объемной температуры на коэффициент трения.

Литература

1. Доценко А.И., Буяновский И.А. / Основы триботехники. Учебник. - М.: Инфра-М, 2014.
2. А. В. Чичинадзе, Э. Д. Браун, Н. А. Буше и др.; Под общ. ред. А. В. Чичинадзе. / Основы трибологии (трение, износ, смазка).  2-е изд. переработ, и доп. - М.: Машиностроение, 2001.