ЖИДКОСТНАЯ СМАЗКА

Гидродинамическая теория смазки

Теория основывается на дифференциальном уравнении Рейнольдса, связывающем давление в смазочном слое с его толщиной, вязкостью и скоростью относительного движения контактирующих тел.

Уравнение Рейнольдса применительно к круглоцилиндрическому стационарно или нестационарно нагруженному подшипнику скольжения имеет вид:

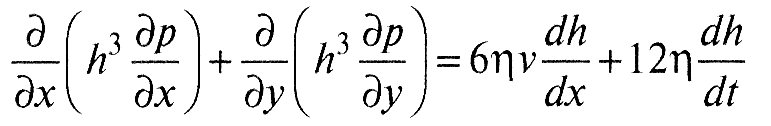,(1)

где p = p(x, у) — давление в смазочном слое; х, у и z — координаты: х — по касательной к внутренней поверхности расточки подшипника, у — параллельно оси подшипника (движение по этой координате отсутствует), z — по толщине смазочного слоя (давление по координате не изменяется), V — проекция скорости по оси х, t — время, h — толщина смазочного слоя.

Предполагается, что давление в смазочном слое определяют силы вязкости, поскольку они много больше, чем силы инерции; смазочная жидкость — ньютоновская; она несжимаема; течение жидкости — ламинарное; поверхности, ограничивающие смазочный слой — абсолютно жесткие, оси вала и подшипника параллельны, смазочный слой полностью заполняет зазор в нагруженной области; течение жидкости в зазоре — изотермическое. Члены левой части уравнения представляют собой расходы смазочной жидкости, обусловленные градиентом давления по осям х и у; правой — изменение расхода этой жидкости за счет изменения формы зазора по оси х и изменения расстояния между поверхностями, формирующими зазор, со скоростью dh/dt, вследствие движения цапфы вала в подшипнике в радиальном направлении.

Граничные условия для этого уравнения имеют вид:

• р = 0 на торцах подшипника;
• р = р₀ в канавках для подачи смазочной среды , где р₀ — давление, под которым подается смазочный материал;
• р ≥ 0 в области существования гидродинамического давления.

Согласно гидродинамической теории теории Рейнольдса, при вращении вала под действием нагрузки Р этот вал располагается эксцентрично в зазоре и смещается в направлении вращения, так что ось, соединяющая центры вала и подшипника, повернута относительно вертикали на угол β (рис.1).

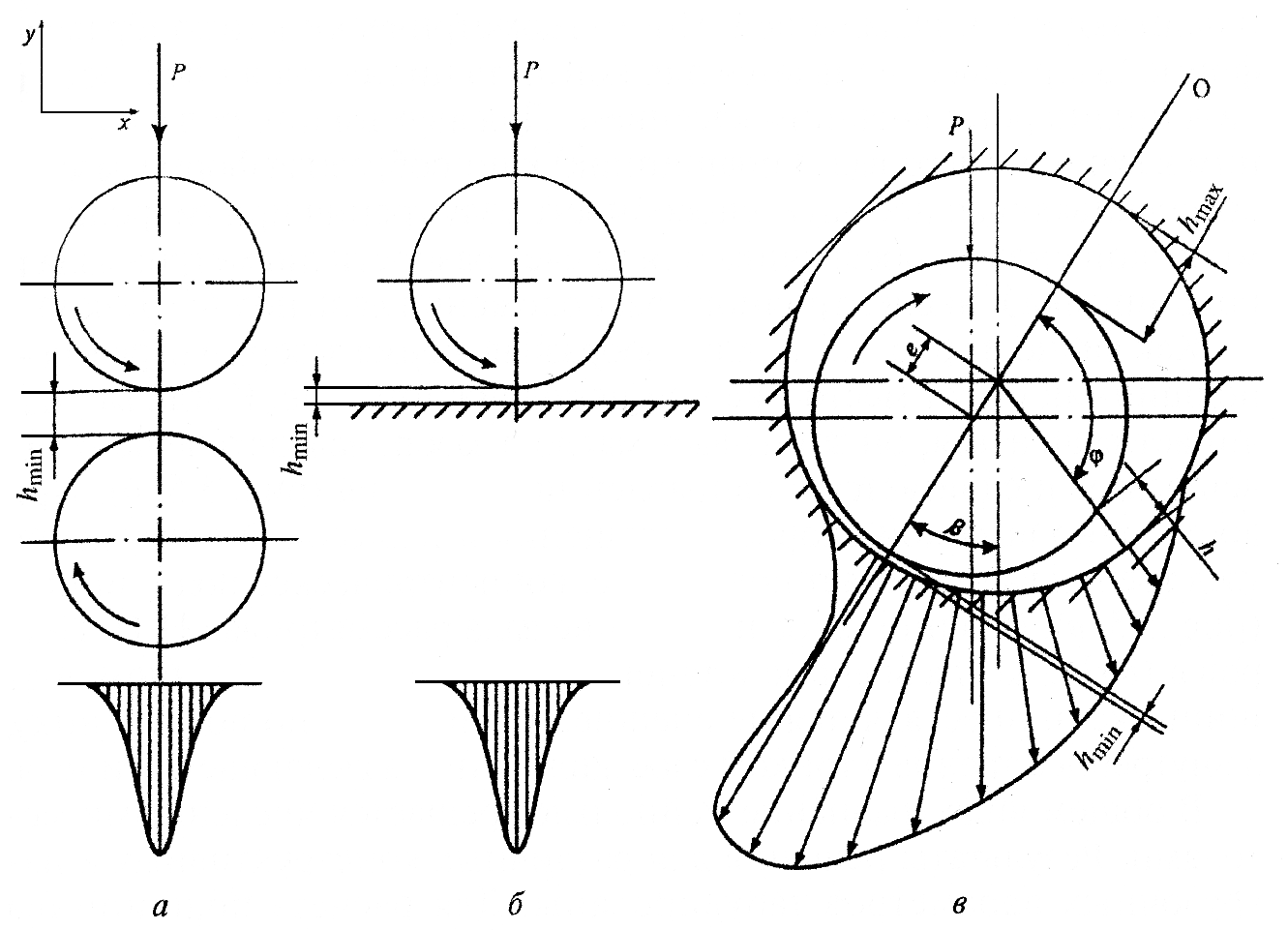
Рис.1. Типичные формы клинового зазора в контакте деталей машин: а — между двумя вращающимися цилиндрическими поверхностями с параллельными осями при внешнем контакте (зубчатые передачи внешнего зацепления, червячные передачи, роликовые подшипники — тела качения и внутреннее кольцо); б — между вращающимся цилиндром и плоскостью (зубчатое зацепление с рейкой, пара кулачок - плоский толкатель); в — две между двумя цилиндрическими поверхностями с параллельными осями при внутреннем контакте (сопряжение вал - подшипник скольжения, зубчатая передача с внутреннем зацеплением, роликоподшипник — тела качения и наружное кольцо).

В общем виде уравнение Рейнольдса не интегрируется, но его можно упростить, допустив, что:

• подшипник скольжения имеет бесконечную длину (вследствие этого отсутствует течение жидкости по оси у);
• оси вала и подшипника строго параллельны (отсутствует девиация).

Тогда уравнение (1) приобретает вид:

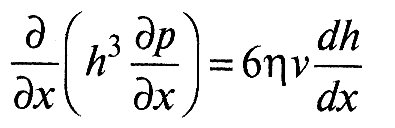,(2)

В интегральном виде это уравнение выглядит следующим образом:

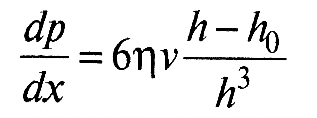,(3)

где h — текущая высота зазора, h₀ — постоянная интегрирования, в данном случае представляющая собой высоту зазора, при которой градиент давления по длине зазора dp/dx = 0 и р = mах.

Анализ уравнений (1—3) показывает, что для возбуждения гидродинамического давления в слое жидкости необходимо, чтобы толщина этого слоя изменялась по направлению движения, уменьшаясь в сторону выхода из контакта. Иначе говоря, гидродинамическое давление в смазочном слое возбуждается при клинообразной форме зазора, получаемой вследствие непараллельности противолежащих поверхностей, образующих этот зазор, и зависит от вязкости жидкости при рабочей температуре и скорости V относительного перемещения рабочих поверхностей. Градиент давления в гидродинамическом слое обеспечивается за счет клиновой формы зазора. Такая форма достигается в плоских подпятниках за счет наклона одной поверхности по отношению к другой, в частности за счет самоустанавливающихся вкладышей. Чисто геометрически клинообразная форма зазора обеспечивается для контакта цилиндра и плоскости и двух цилиндров с внешним касанием . Для двух цилиндров с внутренним касанием (пара вал - подшипник) клинообразная форма зазора, обеспечивающая несущую способность узлу трения при гидродинамической смазке, обеспечивается за счет разности диаметров вала и подшипника и эксцентричного расположения вала под нагрузкой.

Как видно из рис.2а, клинообразная форма зазора в паре вал - подшипник имеет место уже при неподвижном вале. Когда вал начинает вращаться, он затягивает масло в зазор, вследствие чего вал всплывает и сдвигается в направлении вращения (рис.2б). При достаточно высокой скорости вращения и невысокой нагрузке на узел трения вал занимает положение, концентрическое подшипнику (рис.2в). Именно такое положение вала рассматривал Н.П. Петров в 1893 г., когда впервые установил, что в хорошо смазанном подшипнике осуществляется не внешнее трение вала по подшипнику, а внутреннее трение в тонком слое жидкости, разделяющем эти тела.

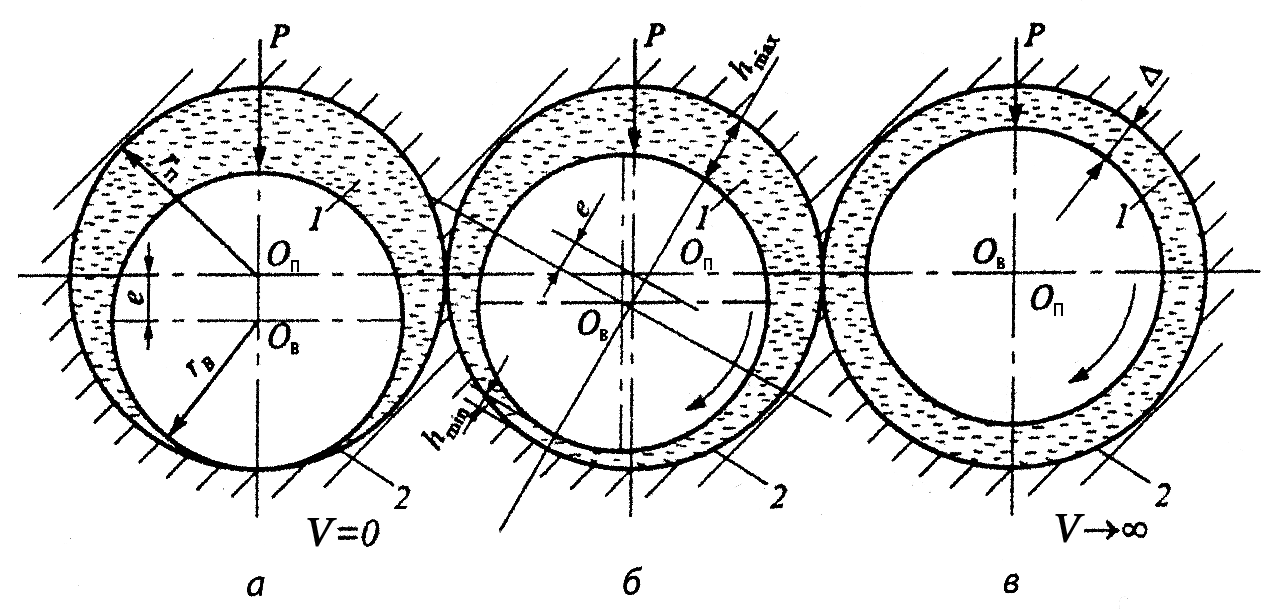
Рис.2. Схема равновесного положения вала 1 в подшипнике 2: а — при неподвижном вале (V= 0); б — при гидродинамическом смазывании; в — при V → ∞ (О_п и О_в — соответственно, центры подшипника и вала; е — эксцентриситет; Р — нагрузка на узел трения; r_п и r_в — соответственно радиусы подшипника и вала; V — скорость вращения вала; Δ — зазор между валом и подшипником; h — толщина смазочного слоя).

В общем виде уравнение Рейнольдса решается численными методами. Результаты решения для различных конструктивных и нагрузочных параметров табулированы. Для расчета подшипника скольжения вначале задаются значения нагрузки на узел трения Р и геометрические размеры подшипниковой пары — диаметр D и длина В, радиальный зазор с между подшипником и валом, а также вязкость η и температура Т₀ смазочной среды на входе. По выбранным параметрам рассчитывают безразмерную характеристику несущей способности смазочного слоя — число Зоммерфельда S₀ (коэффициент нагруженности)

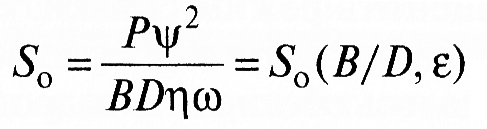,(4)

где относительный зазор ψ = c/R₁, ω — угловая скорость.

По величине S_о с помощью построенных на основе решения уравнения Рейнольдса диаграмм или таблиц (табл.1) определяют соответствующее значение относительного эксцентриситета ε = е/с, где е — абсолютный эксцентриситет — расстояние между центрами подшипника и вала. При расчете следует использовать значения эффективной вязкости, т.е. вязкости при температуре эксплуатации, которую при расчете радиального стационарно нагруженного подшипника бесконечной протяженности можно оценить из уравнения теплового баланса.

Таблица 1. Гидродинамические характеристики подшипника скольжения (при угле охвата подшипника 360° и отношении B/D = 1,0)

Sо	ε	β°	f/ψ	q
0,242	0,2	74,2	12,958	0,039
0,611	0,4	62,57	5,787	0,078
1,318	0,6	50,454	3,210	0,116
3,5958	0,8	36,028	1,691	0,1533
8,520	0,9	26,368	1,046	0,1708
19,799	0,95	18,639	0,660	0,1783

S₀ — число Зоммерфельда; ε — относительный эксцентриситет; β° — угол наклона центров; f/ψ — относительный коэффициент трения; q — удельный расход жидкости через узел трения.

При решении неизотермической задачи уравнение Рейнольдса применяют в более общем виде и к нему присоединяют уравнения теплопереноса.

Затем рассчитывают искомое значение минимальной толщины смазочного слоя по линии центров

h_min = c(1- ε), (5)

сравнивая которое со значениями параметров шероховатости контактирующих тел делают заключение о возможности реализации гидродинамической смазки. Предварительно необходимо проверить по величине числа Рейнольдса, является ли течение жидкости в зазоре ламинарным. Это необходимо, поскольку уравнение Рейнольдса выведено применительно к условию ламинарного течения жидкости.

Решение уравнения Рейнольдса позволяет оценить минимальную толщину смазочного слоя h_min. Затем из уравнения (6) по величине критерия λ следует оценить режим смазки. Если при выбранной макро- и микрогеометрии пары трения и рассматриваемой вязкости смазочной среды не удалось обеспечить гидродинамический режим смазки, то эти факторы следует скорректировать (например, обеспечить большую гладкость поверхностей трения).

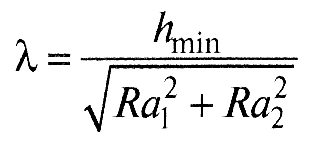, (6)

Для расчета гидродинамического подшипника скольжения следует также рассчитать величину коэффициента трения, для того чтобы оценить потери на трение, а также рассчитать температуру масла. Это сделать необходимо, поскольку важнейшая характеристика смазочной жидкости — ее эффективная вязкость — сильно зависит от температуры. Кроме того, во многих случаях существуют ограничения на предельную температуру масла в процессе работы машины.

Уравнение для расчета коэффициента трения в нагруженных подшипниках скольжения получено на основе интегрирования уравнения Рейнольдса применительно к подшипнику бесконечной длины. Оно имеет вид:

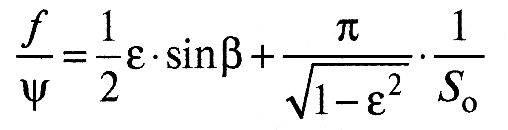, (7)

Здесь безразмерные соотношения f/ψ, ε и угол β — величины табличные (см. табл.1) и определяются по величине коэффициента нагруженности S₀, который рассчитывается по формуле (4).

При ε → 0, т.е. при совпадении осей вала и подшипника, уравнение (5) превращается в формулу Н.П. Петрова. Эту формулу он вывел в 1883 г., допустив, что вал и подшипник соосны (эксцентриситет е = 0), что близко к реальности в случае весьма легко нагруженного подшипника при высокой частоте вращения вала.

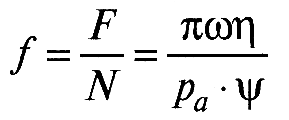, (8)

где F — сила внутреннего трения, N — нагрузка на узел трения, ω — угловая скорость, р_а — номинальное давление в контакте, η — динамическая вязкость, ψ — относительный зазор.

При этом следует иметь в виду, что коэффициент трения в уравнении (5) и формуле (7) принципиально отличается от коэффициента внешнего трения и лишь формально может так называться.

Гидростатическая смазка

В ряде случаев возникает необходимость осуществления жидкостной смазки некоторых узлов трения, но в то же время выдвигаются условия, которые делают невозможным или недопустимым решение этой задачи путем организации гидродинамического режима. К таким условиям относится требование осуществить жидкостную смазку при малой скорости относительного перемещения контактирующих тел (или вообще при отсутствии их относительного перемещения) и при нагрузках на узел трения, превышающих грузоподъемность гидродинамического слоя, требование низких и постоянных коэффициентов трения и/или минимальных износов трущихся тел при любых режимах работы узлов трения (при пуске и остановке режим смазки меняется, переходя от граничной и смешанной к гидродинамической и наоборот, что приводит к значительному изменению коэффициентов трения и наличию износов при граничной смазке). В таких случаях прибегают к организации гидростатической смазки, т.е. жидкостной смазки, при которой полное разделение поверхностей трения деталей, находящихся в относительном движении или покое, осуществляется жидкостью, поступающей в зазор между этими поверхностями под внешним давлением. Схема узла трения (в данном случае — упорного подшипника с центральным расположением кармана) приведена на рис.3. Вал, заканчивающийся несущим фланцем 1, опирается на буферную пластину 2, в которой по оси выточен масляный карман 5. По оси к валу приложена нагрузка Р. Через отверстие в буферной пластине насос, расположенный отдельно от узла трения (на рисунке не показан), под давлением р₀ подает рабочую жидкость, которая заполняет карман 5, раздвигает опорные поверхности на высоту h и радиально вытекает из образовавшегося зазора. Давление р₀ создаваемое насосом по площади дна кармана ωr_к², и переменное давление р, действующее по остальной поверхности подшипника, обеспечивают грузоподъемность смазочного слоя, достаточную для уравновешивания осевой нагрузки Р (рис.4).

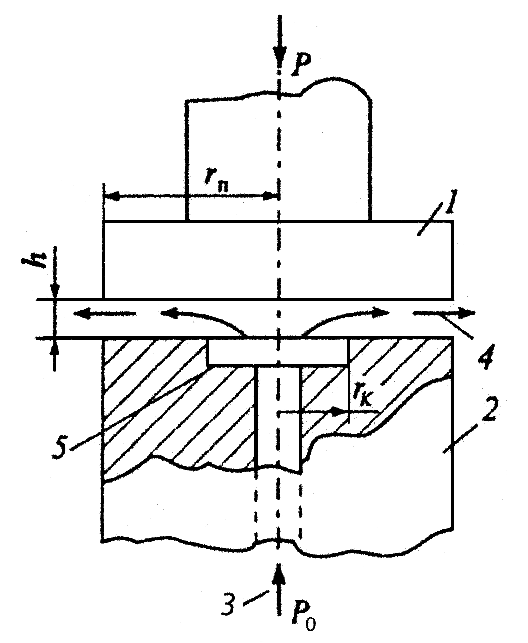
Рис.3. Схема гидростатического подшипника (по Д. Муру): 1 — фланец вала; 2 — буферная пластина; 3 — подача масла; 4 — слив масла; 5 — масляный карман.

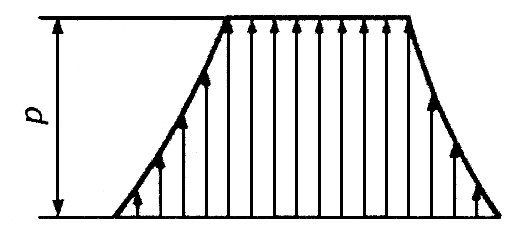
Рис.4. Радиальное распределение давления р смазочной жидкости по поверхности гидростатического подшипника.

Несущая способность подшипника не зависит от скорости относительного перемещения тел и вязкости масла и определяется конструктивными размерами подшипника (соотношением между радиусом фланца и радиусом кармана) и подаваемым давлением. Таким образом, при пуске-останове узла трения обеспечиваются жидкостная смазка и отсутствие износа рабочих поверхностей. При увеличении нагрузки на узел трения уменьшается величина зазора h между сопряженными поверхностями, возрастает скорость истечения смазки из кармана, что ведет к повышению давления р. Это, в свою очередь, ведет к увеличению несущей способности гидростатической опоры.

Таким образом, несущая способность подпятника рассчитывается как

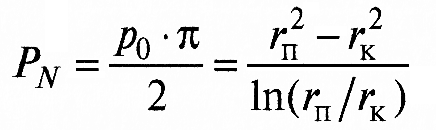, (9)

Распределение давлений в смазочном слое гидростатического радиального подшипника при невращающемся вале оценивается из уравнения Рейнольдса при нулевой правой части

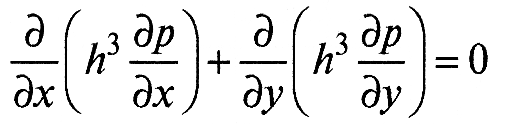, (10)

В настоящее время ассортимент гидростатически смазываемых узлов трения достаточно велик. Кроме обеспечения несущей способности при малой скорости относительного перемещения, очень малых потерь на трение, отсутствия износа сопряженных тел гидростатические опоры обеспечивают большую точность вращения, высокую жесткость и динамическую устойчивость и наличие хороших демпфирующих свойств. Эти свойства гидростатических опор обусловили их применение в подшипниках прокатных станов, гидротурбин, генераторов, в различных опорах и направляющих металлорежущих станков, причем при увеличении размеров станков эффективность применения гидростатической смазки, как правило, повышается. В частности, гидростатическое смазывание используют в круговых направляющих планшайб диаметром до 12 м, направляющих прямолинейного перемещения ползунов, кареток, стоек с величиной перемещения в несколько десятков метров, радиальных опорах диаметром до 5 м, а также в передачах червяк-рейка и винт-гайка.

Разнообразие узлов трения, в которых применяют гидростатическое смазывание, обусловливает разнообразие конструктивных решений, применяемых для его реализации. Общим во всех случаях является, как в рассмотренном нами случае, наличие карманов в одной из сопряженных поверхностей узла трения. Через эти карманы подается под давлением рабочая жидкость, осуществляющая разделение этих поверхностей.

Гидростатические опоры могут иметь плоскую, цилиндрическую, коническую, сферическую или другую форму. В радиально-упорных гидростатических подшипниках комбинируют плоскую и цилиндрическую формы контактирующих поверхностей.

Коэффициенты трения в гидростатических подшипниках имеют тот же порядок, что и в других узлах трения, смазываемых жидкостной смазкой.

Эластогидродинамическая смазка

К 1940-м гг. было установлено, что в тяжелонагруженных или неприработанных смазанных узлах трения — зубчатых и цепных передачах, подшипниках качения, полимерных легкодеформируемых подшипниках скольжения, при обработке металлов давлением — при определенных условиях имеет место жидкостная смазка, хотя толщина рассчитанного по уравнению Рейнольдса смазочного слоя не превышает суммарной высоты неровностей контактирующих тел, так что можно было предположить режим граничной смазки. Это явление объяснено эластогидродинамической теорией смазки. Идеей теории является распространение классической теории гидродинамики на условия контакта, при которых высокие давления на узел трения упруго деформируют контактирующие тела и увеличивают вязкость смазочного материала в пленке жидкости, разделяющей эти деформированные тела. Эти два явления (упругая деформация твердых тел и увеличение вязкости масла) приводят к существенному росту толщины смазочного слоя. При эластогидродинамической смазке толщина слоя масла, разделяющего поверхности трения, может на два порядка превышать толщину смазочного слоя, рассчитанного для этих условий по классической теории Рейнольдса, и этот слой выдерживает существенно большие давления, чем гидродинамический слой по Рейнольдсу, когда смазочный материал постоянной вязкости разделяет абсолютно жесткие поверхности трения.

При высоких давлениях, вызывающих упругие деформации контактирующих поверхностей (что обычно характерно для контакта неконформных деталей) и заметное повышение вязкости смазочной среды, минимальную толщину смазочного слоя оценивают из уравнений ЭГД-теории, полученных совместным решением гидродинамического уравнения (3), уравнения упругих деформаций, уравнения, описывающего тепловое состояние смазочного слоя, и уравнения, описывающего зависимость вязкости смазочной среды от давления (или от давления и температуры) обычно по формуле Баруса, согласно которой η(p)=η₀exp(αp), где η₀ — вязкость масла при атмосферном давлении, α — пьезокоэффициент вязкости этого масла. Обычно стремятся упростить расчет, не учитывая влияние температуры на вязкость.

Толщина смазочного слоя в контакте двух катящихся цилиндров при изотермическом рассмотрении (рис.5) определяется, согласно А.И. Петрусевичу:

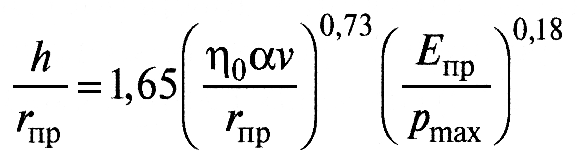, (11)

где r_пр и E_пр — соответственно приведенные радиус кривизны контактирующих цилиндров ( r_пр=(r₁*r₂)/(r₁±r₂), плюс относится к внешнему касанию, минус — к внутреннему) и модуль упругости их материалов; р_max — максимальное давление в контакте по Герцу; η₀ и α — динамическая вязкость и пьезокоэффициент вязкости базового масла при температуре входа в контакт; V = (V₁+V₂) — окружные скорости контактирующих цилиндров.

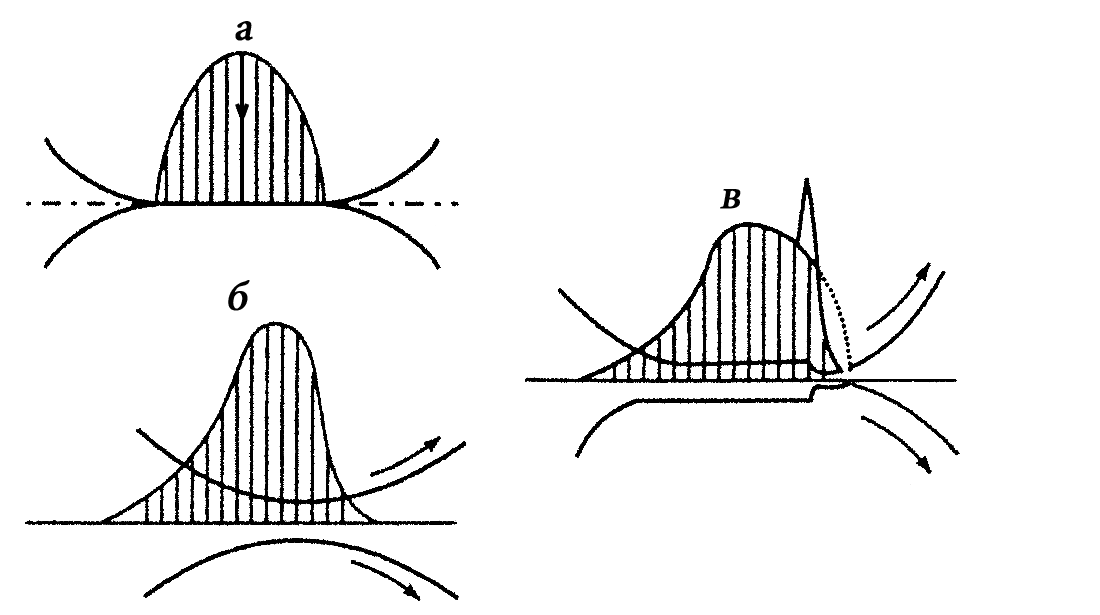
Рис.5. Схема изотермического контакта двух гладких цилиндров: а — без смазочного материала (цилиндры упругие); б — профиль гидродинамического давления на входе (цилиндры абсолютно жесткие); в — профиль давления и смазочного слоя при эластогидродинамической смазке (цилиндры упругие).

Заметное влияние тепловых явлений на толщину h_т смазочного слоя в ЭГД-процессе можно по рекомендации Ю.Н. Дроздова учесть, введя тепловой фактор Ф_т

h_т = hФ_т, (12)

где величина h определена по формуле (11) для изотермического процесса ЭГД-смазки.

При этом

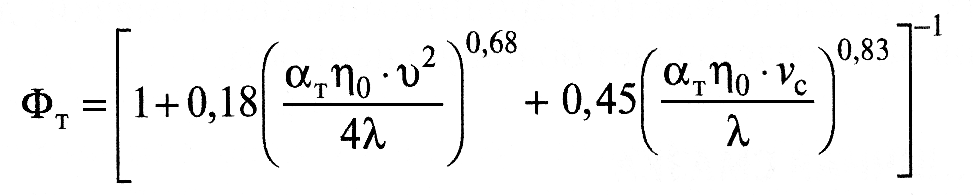, (13)

где α_т и λ — соответственно, параметр зависимости вязкости масла от температуры и коэффициент теплопроводности масла, V_c — скорость скольжения в ЭГД-контакте.

Анализ полученных уравнений эластогидродинамики позволяет установить физическую картину, имеющую место в эластогидродинамическом контакте. Она схематически приведена на рис.5 применительно к упругому контакту по образующим двух цилиндров с параллельными осями. При контакте двух неподвижных цилиндров эпюр давлений соответствует теории Герца.

При относительном перемещении трущихся поверхностей значительные давления, действующие в зоне контакта, приводят к тому, что в центральной части заполненного смазочным материалом зазора вследствие упругих деформаций участки контактирующих поверхностей становятся почти параллельными, вязкость смазочного материала в зазоре повысится. Гидродинамическое давление на входе в зазор будет меньше герцевского. Естественно, объемный расход жидкости в щели с плоскими стенками и ее скорость будут постоянны. На выходе из зазора герцевское давление резко падает, и вязкость значительно (на несколько порядков) снижается до ее значения при атмосферном давлении. Одновременно снижение герцевского давления приводит к уменьшению ширины зазора и соответственно — снижению толщины смазочного слоя. Требование неразрывности потока приводит к значительному росту скорости течения жидкости. Гидродинамическое давление на выходе резко возрастает, имеет место так называемый «пик давления», теоретически предсказанный А.И. Петрусевичем и подтвержденный экспериментально. По величине «пик давления» зачастую превышает максимальное герцевское. Наличие «пика давления» оказывает определенное влияние на контактную прочность деталей, работающих в режиме эластогидродинамической смазки, а быстрое прохождение смазочного материала через область высокого давления вызывает явления, отличающиеся существенной нестационарностью.

Изометрическая задача эластогидродинамической смазки была решена А.М. Эртелем (1939) и А.Н. Грубиным (1949). Исходя из ряда упрощающих допущений они вывели уравнение для определения толщины эластогидродинамического смазочного слоя. Эта величина (обычно составляет от 0,1 до 10 мкм) является решающей при идентификации режима смазки, поэтому при расчетах узлов трения, работающих в режиме эластогидродинамической смазки, для конструкторов она представляет большую ценность.

Литература

1. Доценко А.И., Буяновский И.А. / Основы триботехники. Учебник. - М.: Инфра-М, 2014.
2. А. В. Чичинадзе, Э. Д. Браун, Н. А. Буше и др.; Под общ. ред. А. В. Чичинадзе. / Основы трибологии (трение, износ, смазка).  2-е изд. переработ, и доп. - М.: Машиностроение, 2001.
3. Гаркунов Д.Н. / Триботехника (конструирование, изготовление и эксплуатация машин): Учебник. М.: МСХА, 2002.
4. В.В. Джамай, Ю.Н. Дроздов, Е.А. Самойлов и др. / Прикладная механика: Учебник для вузов. М.: Дрофа, 2004.